We have
a method
to create the most reliable software ever invented
a method
to create the most reliable software ever invented
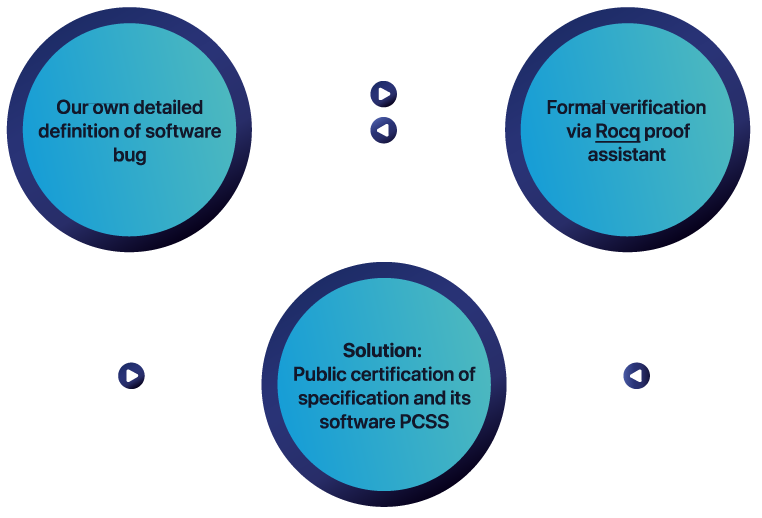
Public Certification of a Specification and its Software (PCSS)
We guarantee the mathematical correctness of your specification and its exact transmission to the final code.
We guarantee the mathematical correctness of your specification and its exact transmission to the final code.

It is not possible to establish a proven equivalence among formal specification and natural language, nor even to any intermediate abstraction level of mathematical language. Those worlds are disconnected. We also have the issue that a sentence in natural language can be interpreted in different ways: natural language is ambiguous. Knowing that, there are chances to find solutions PCSS.
Guillermo Errezil (Director)
Guillermo Errezil (Director)
Our philosophy
If we want to create perfect software, we would not write a single line of code, just focus on technical and formal specifications. The code is obtained by the formally verified extraction mechanism.
In accordance with this choice, we are committed members of the Rocq Consortium and we contribute new features to both Rocq and MathComp. We have a method to create the most secure software ever invented.
If we want to create perfect software, we would not write a single line of code, just focus on technical and formal specifications. The code is obtained by the formally verified extraction mechanism.
In accordance with this choice, we are committed members of the Rocq Consortium and we contribute new features to both Rocq and MathComp. We have a method to create the most secure software ever invented.
What software bugs does the PCSS method solve?
|
1
|
We can prove that what the developer intended (in any abstraction language) is computable. | |
|
2
|
We can prove that what the developer intended is exactly done by the software. | |
|
3
|
We can control point 2 and somehow control before deployment the unexpected consequences of what the developer intended, if there are unintended consequences that may be considered wrong. | |
|
4
|
We can prove that what the developer intended has no direct mathematical issues, incorrectness, inconsistency… | |
|
5
|
We solve the issue of testing: no need. | |
|
6
|
We solve the issue of expressivity: we can express every mathematical statement in Rocq . |
What software bugs does the PCSS method not solve?
|
1
|
In some cases, we cannot solve whether the specifications made by the developer are enough to fulfill what the developer has in mind. |